An introduction to the mathematical processes of Collision Drive Theory
Siize Gabriel Punabantu
Tier 1 Gravity Device
18 February 2021
Introduction
This document introduces the basic mathematical processes
of a Collision Drive (C-Drive) [patented]. The C-Drive mechanism is
reverse engineered to reproduce how atomic particles generate mass and use it to
create gravitational force that can be harnessed for propulsion. This gravitational force is referred to as Tier 1 Gravity and is reproduced using mechanical engineering.
 |
| Collision Drive [Patented] |
 |
Collision Drive [C-Drive] source: Pacra Patent |
Conventional application of the equation for
inelastic collisions
The total momentum before the collision is M1V1+M2V2 is
equal to M1Vf+M2Vf after the collision. Where Vf is the final velocity.
The equation above states the velocity before collision
is equal to the combined velocity after the inelastic collision.
Since Vf is common and the two masses move together after the inelastic collision the right side of the equation can be reduced.
M1Vf +M2Vf can be reduced to Vf (M1+M2)
Therefore:-
M1V1+M2V2 = Vf (M1+M2)
M1 – mass of 1st object before collision,
object is moving
V1 – velocity of 1st mass
M2 – mass of the stationary or second object
V2 – velocity of second mass which is stationary at the
beginning
M1:[Vf] – 1st mass after collision
M2[Vf] – 2nd mass after collision
Adapting the above Equation from Collision
Theory to the C-Drive
The following notation is applied:
M1blV1bl+M2brV2br+M3blV3bl
= Vf(M1al+M3al)
Where “b” – before collision, l – linear collision,
r rotation
And
M1bl is the linear value of the 1st
mass before collision
V1bl is the linear velocity of the 1st
mass before collision
M2br is the rotational value of the 1st
mass before collision
V2br is the rotational velocity of the 1st
mass before collision
M3bl is the linear value of the 2nd
mass before collision
V3bl is the linear velocity of the 2nd
mass before collision
After collision
Where “a” – after collision
M1al is the linear value of the 1st
mass after collision
V1al is the linear velocity of the 1st
mass after collision
M2ar is the rotational value of the 1st
moving after collision
V2ar is the rotational velocity of the 1st
mass after collision
M3al is the linear value of the 2nd
mass after collision
V3al is the linear velocity of the 2nd
mass after collision
Vf – final velocity
M1bl V1bl + M2br V2br
+ M3bl V3bl = Vf(M1al + M3al)
Therefore;
Vf =
M1bl V1bl + M2br V2br + M3bl
V3bl / M1al + M3al
or
Note that there is no division by M2ar. To do so
would be incorrect as M1al and M2ar are the same object. Since
the equation above is for both a single linear and rotating mass, for the C-Drive
substitutions are made to accommodate collisions from a rotating mass highlighted
in bold in the centre of the equation in brackets as follows.
The highlighted section in the centre of the Vf equation [M2brV2br]
We know that;
Fc = ma
Where m- mass, a - acceleration
This can be further expressed mathematically as;
Where Fc is centripetal force, v2 is acceleration and r is the radius of rotation.
This equation is for a rotating mass therefore to make it easier
to understand it is best to work out the rotational velocity separately:
Where d – is distance such that md – distance in meters, s – time in seconds
Substituting velocity (v) in the equation with its
rotational expression we get:
For increased clarity this can also be expressed using the collision equation notations as
Take note that:
Mb1l – in the equation for
inelastic collisions is the linear value of the 1st moving mass before the
collision
r – is the radius of rotation
v – is the velocity of
the mass M2br as it rotates
s – time in seconds
md –
distance in meters
Fc – rotating (centripetal
or centrifugal) force
Amplification
of Force
Amplification takes place when the 60kg mass is rotated. Since the 60Kg mass is being rotated at 240 rpm it is travelling at a velocity of 22.98 m/s. At this speed the 60kg mass experiences amplification and now exerts a kg-force of 3,533.55Kg, equivalent to 34,642.69 Newtons. Therefore, note that the mass of the entire vehicle is 1,560kg whereas the collision force from M2b exerted is 3,533.55Kg or 34,642.69 Newtons, however, its inherent mass remains 60Kg. The C-Drive is generating a greater propulsive force than itself combined with the entire mass of the vehicle.
M1bl – is 60kg (Remember that M1bl
and M2br are the same object or mass and therefore this mass should
not be duplicated during division in the collision equation.)
V1bl – is 0 m/s (initial linear velocity before
collision)
M2br – 60kg (or 3,533.55Kg during rotation at 22.98 m/s or 240 rpm)
V2br– 22.98 m/s
M3bl – 1,500Kg is the mass or weight of the vehicle
V3bl – 0 m/s (initial linear velocity before
collision)
Propulsive Force is applied through 0 - 360 degrees
of rotation
Where Vf is the signature applied by the mass to generate thrust or lift. Note that the equation above is an introductory equation and therefore only applies a signature with the 1st amplification of force (60Kg to 3,533.55Kg or 588 Newtons to 34,628.79 Newtons). There are 3 more stages of amplification.
Note that the rotational
speed is 240 rpm or 4 rotations per second (rps) therefore in the 1 second in
the equation 4 rotations have occurred giving a ratio or count 1:4 which
requires 5.7362 to be multiplied by 4 to accurately cover and convey the 1
second duration and this has to factored in.
1,560 kgl is converted into Newtons to find the final
combined velocity of the collision-drive and vehicle.
After the launch collision the vehicle begins to move. It is no longer stationary therefore the velocity 2.27 m/s and each increase in velocity thereafter, like a chain reaction, must be factored into the subsequent equations for [M2arV2ar] by applying the change in velocity to M1al[V1al] and M3al[V3al] to cumulatively apply increases in velocity from each collision over time.
Should the vehicle maintain the launch velocity of 2.27 m/s by maintaining a constant rpm the vehicle will continue to increase speed and accelerate at 2.27 m/s^2* (in exactly the same manner as gravity from which the C-Drive is reverse engineered) despite the rpm and fuel applied to sustain the rpm remaining constant. These gains are from engineered mechanical efficiency.
* This should provide sufficient proof that gravity is primarily generated by mechanical engineering, or mechanical processes rather than fields. Fields are a "field effect" of these processes.
Since [V1al] and [V3al]are the same value they can be worked out together in the equation as Vl(M1al+M3al) where Vl becomes the constant for combined acceleration after collisions, in this case 2.27 m/s with the understanding that should the throttle fall or increase and rpm drop or rise Vl will change accordingly affecting the s/m^2 velocity of the vehicle. This allows a vehicle to be moved very gently, with great precision at low speeds and for it to launch at appropriately high velocity where required.
Each increase in velocity after each collision that moves the vehicle and C-Drive must be factored into the equation in this way as demonstrated in the table below in the column for combined cumulative velocity.
Drop Test
During the manufacture of the C-Drive a non-motorized Drop Test was performed on it. This is where, before being harnessed to a vehicle chassis, the C-Drive's 60kg mass was raised and allowed to fall or drop under gravity simulating rotation and a launch collision. The drop caused the C-Drive to surged forward with remarkable acceleration. The results were impressive to say the least. The acceleration on observation seemed unnaturally strong and can be described as a "surge" or forward "lunge". This result is what encouraged the vehicle chassis to be built, the engine to power it acquired and the C-Drive hitched to the chassis in preparation for it to be fully motorized. The results will be shared after mid to end of the year tests as has been mentioned.
Acceleration
Note that despite the C-Drive maintaining a constant 240 rpm the equations show the vehicle steadily accelerates over time as seen in the column for combined cumulative velocity reaching 27 m/s in 1.5 seconds also shown in Km/h and Mph in the table above. The C-Drive will allow significant propulsion to be gained even at very low rpm.
Its also important not to expect a C-Drive to generate acceleration in the same way that a jet engine, rocket engine or torque from an engine generates acceleration. These technologies differ from that of a C-Drive and are best used as powerplants rather than the means of propulsion. How the different technologies manage conservation of momentum is completely different. These other technologies use energy directly to propel a vehicle and its mass, on the other hand energy drives the C-Drive, which then propels the vehicle allowing for amplification between the energy source and the the source of propulsion increasing mechanical efficiency. A C-Drive has several stages of amplification of propulsive force, while the other systems have none. The equations in this document only introduce the 1st stage of amplification of propulsive force. The C-Drive operates and mimics gravitational acceleration whilst the other propulsion systems do not. This topic is for a mechanism that will spawn an area of science in and of itself, it is extensive and will need to be delved into in more depth at a later time, to avoid spoilers - so to speak.
At a constant of 240 rpm the C-Drive is designed in such a way that the vehicle or load (M1al-M3al) are propelled with the same force after each collision (3,533.55 kg-force or 34,642.6 Newtons). This ensures that the rate at which acceleration grows or accumulates over time or per second is a constant (i.e. 2.27 m/s^2) seen in the Combined Cumulative Velocity column.This demonstrates that the gains in acceleration are constant, that velocity will continue to increase over time without the need for an increase in rpm and is caused by mechanical efficiency. The implications of this on maximum velocity is discussed here. Although a constant rpm is used in this example note that a C-Drive is also designed to be able work with variable rotational speeds from 0 rpm upward giving very precise control of a vehicle’s velocity and movement.
Constant velocity will give C-Drives an advantage when working their way to escape velocity for launches from earth into space since they would accelerate in the opposite direction of gravity in a manner that uses mechanical efficiency (i.e. per second per second acceleration) rather than fuel to equal and in some cases exceed the per second per second efficiency and pull of gravitational force that plagues launches. This will be a major advantage for activity related to Space.
In the configuration above the C-Drive is designed to only need 240 rpm to achieve 0-60 in 1.5 seconds. This should be indicative of gains from this being a more efficient propulsion technology. A C-Drive doing 0-60 in 1.5 seconds may not sound impressive, but try doing this in your ride but do so while keeping the rpm on your rev-counter constant at 240 rpm. The performance of the C-Drive's propulsive force can be raised by increasing the device's mass (M1bl which is the same object as M2br) e.g from 60Kg to 240Kg or 400kg, or by simply increasing rpm. For instance, increasing the mass of the C-Drive from 60kg to 240kg and maintaining 240 rpm will improve 0-60 from 1.5 seconds to 0.5 seconds.
Adjusting gearing ratios between the engine rpm and C-Drive rpm can allow them to run at equal speeds 1:1, or have the engine run faster >1 or slower <1 than the C-Drive. It should be noted that 240 rpm is a very conservative value as modern engines idle at around 1,000 rpm, are capable of rpm in excess of 5,000 and electric motors are capable of rpm as high as 25,000. It should also be noted that large jet engines are capable of rpm in the range of 10,000 - 25,000 while micro turbines and smaller turbine designs can reach rpm in the range of 100,000 to 500,000.
Normally the high rpms of an engine or powerplant are used directly to move a vehicle which weighs a considerable amount, in some cases several tonnes, leading to a highly inefficient method for propulsion. When the powerplant is harnessed through a C-Drive the propulsive force is increased tremendously. Applying alternative masses and rpms to the equations and method above will demonstrate this. Having the technology to control and generate acceleration in the same manner gravity does by reverse engineering it as has been done with the C-Drive will be indispensable to humanity's progress on Earth and in Space. Human beings are comfortable in constant acceleration at 9.8 m/s2. However, unmanned flights can be sent as advance scouts to, for instance, determine the suitability of Earth-like planets for human habitation that have been recently discovered. In these circumstances unmanned craft can travel at very high rates of constant acceleration 100 m/s2 or 1,000 m/s2 to try to get to these destinations in days rather than over decades. This means that even habitable planets or Earth IIs that have been recently discovered but thought to be unreachable because they are light-years away can now be reached using C-Drives in very short periods of time.
Many physicists have stated that the speed of light is a universal limit and cannot be exceeded. There is also the hypothesis that mass becomes infinite as the speed of light is reached. The equations above show that C-Drives are a propulsion technology that can be used to very easily test the validity of the limits and accuracy ascribed to luminal velocities that prevail in science today. To put these arguments to rest, whether this limit is true or false can be very easily tested today using the propulsive technology of C-Drives. Many physicists have weighed in their views on this topic and it will be interesting to see who got it right and who got it wrong.
The other advantage of C-Drives is that their fuel efficiency means that humanity does not need to wait for exotic fuels to be created such as nuclear energy, fission and so on to travel these extra-ordinary distances. In the present they can be covered by a mix of conventional renewable and non renewable fuels already in use.
Flight: Thrust
to Weight Ratio (TWR)
By far exciting prospects are for the use of the C-Drive in cars, airlines or transportation in general and in space launches and exploration. The means for determining flight for the device requires it pass a thrust to weight ratio assessment.
The thrust
to weight ratio (TWR) is
 |
It should be noted that in this example the mass of the vehicle is 1,500kg and the mass of C-Drive is 60kg. The total or combined mass of the entire vehicle is 1,560kg. In order to work out the thrust to weight ratio these values are both expressed in kiloNewtons. The force of the rotating mass and its load at 240 rpm are expressed as 34.6kN while the weight of the vehicle (1,560kg) is expressed as 15.29kN. The C-Drive can be designed to any spec (in terms of size: it can be miniaturized or supersized) depending on where and how it will be used.
For the sake of example, the red sports car used to illustrate how flight will take place weighs 1.5 tonnes or 1,500Kgs and is propelled by four small C-Drives (with a diameter of 0.3 meters); with the combined volume, radius, attributes and weight of 60Kg we have seen in the single C-Drive above. For this example the TWR of the values above can be worked out as follows;
As shown above as long as the TWR is greater than 1 the red sports car or any type of vehicle and its load will be lifted off the ground. A C-Drive is designed to be capable of very precisely controlling the TWR allowing for increased maneuverability, buoyancy and feather-like landing and take-off for V-Tol capabilities, yet it maintains the ability to launch at very high velocities. In addition to this a C-Drive is able to create propulsion with constant acceleration. It can launch at any level of g-force and maintain the rate through mechanical efficiency. In other words if its launch velocity is 1g, 1.9gs, 9.8gs, 500gs, 1,000gs, 1 million gs, 30 million gs or more (launching instantly at high velocities such as 30 million gs and higher will not be a significant task for purpose built Collision Drives), furthermore the equations will show it can maintain rising velocity at a constant rpm without this placing a strain on resources or the propulsion system itself. Note that 30 million gs is only 3 million kg-force (approx 29,500 kN). It takes only 7,000 rpm to amplify 60 kg to 3 million kg-force.
Increasing the mass of the C-Drive from 60kg to 240kg whilst maintaining 240 rpm will raise the TWR to 8. Elevating the throttle from low 240 rpm to 2,520 rpm whilst maintaining 60kg would cause the C-Dive to increase the TWR from 2.27 to 250. At 5,000 rpm the TWR is 980.
The equations above can be used to try different configurations. The results of the equations for Thrust To Weight Ratio (TWR) attest to the C-Drive's capacity for flight and being in class of its own when it comes to its ability to create buoyancy, generate lift and move significant loads.
Conclusion
If the equations in this introduction are understood then you now have a decent idea of the basic operations of a C-Drive and the equations you need to know to appreciate how it works. This should enable you to understand, for instance, that if you need to move, shift or lift a payload of a billion tonnes contemporary propulsion systems would require engineers to build a motor, engine, or rockets equal to this load leading to highly inefficient methods. This is not how a C-Drive works. If it is purpose built to ferry a billion tonnes or lift it into space engineers only need to build a C-Drive that can process 500 kgs per millisecond, consequently amplifying the the mass which is then capable of effortlessly moving the payload. To be precise 500 kgs per millisecond will lift and transport 1.84 billion metric tonnes efficiently.
Not only is a C-drive capable of very gentle movement, it is also capable of launching at and maintaining tremendous velocities, some of which will not be suitable for manned flight and yet in addition to this it is capable of rendering buoyant or lifting tremendous loads over land and into space, the limits of mass and rpm can be applied to forecast results.
The first stage of amplification observed in the C-Drive is spin at the centre of the equation represented by M2brV2br which saw its mass of 60 kg amplified to 3,533.55Kg and applied to propulsion. However, there are three further stages of amplification that have been identified that further increase this propulsive force. These are directly related to how the mechanism works and will allow scientists to "tune" or tweak the device to maximize its performance very much the way engines are tuned with similar objectives. Although the first stage of amplification seems ample enough, the immediate consequence of further amplification in the other stages is significant increases in lift capacity, velocity, torque and acceleration than what has, for the time being, been introduced here. The most important benefit of the further stages of amplification appear to be most useful in their ability to offer a solution to the immense distances between destinations in Space by dramatically shortening travel times for instance between habitable planets that have been recently identified.
These distances require a means of acceleration equal to the task, and it appears the C-Drive, which is reverse engineered from gravity naturally addresses these constraints through the enhancements in acceleration offered by these further stages. The equations above will show that purpose built C-Drives have the quickest 0% - 99% [of the speed of light] of any propulsion system currently available to the scientific community, with the advantage being that vessels propelled by the device placed in a convenient orbital path around the earth can have scientific apparatus and a diverse array of instruments on board to provide humanity feedback in real time concerning what occurs on a vessel during this type of acceleration. The advantage of a C-Drive propulsion system powerful enough to approach 99% and powerful enough to test pushing through this boundary is that it remains in close enough proximity for data from tests to be communicated to scientists on earth. These tests are significant to the well-being of humanity, can be conducted today and empirical results obtained at reasonable cost. Depending on the rate of acceleration through the orbital path these can be manned or unmanned tests to gain empirical evidence that include constant acceleration at 1g. There are technical aspects of a C-Drive apparatus and method that have been left out of the equations and methodology in this introduction that make it faster, more efficient and much more powerful as a propulsion technology than is demonstrated by the equations above. These can be explained and introduced at a later time.
C-Drives can be designed to have mobility in any direction in three dimensional space where they can move safely and with exceptional agility and accuracy. They can be designed and built for very large installations to move heavy loads, but they can also be built for high rates of acceleration and speed or for use in micro-applications where movement can be exceptionally nimble and controlled, for example, in medical science. Miniature or Micro C-Drives, like gyros installed in a smart phone, entail that when a mobile phone receives a call it can navigate through rooms to its owner who then picks up the call. The functionality, applications, uses and areas of industry C-Drives can be applied to are innumerable with significant potential for broadly enhancing and expanding the scope of how engineering in diverse sectors is applied and used to improve the human experience.
This is a very
basic introduction to the mathematics behind a C-Drive. A C-Drive is a simple,
but ingenuously designed device that is likely to spawn a field of study or field of science of
its own that intrinsically catalogues what it does and how it works as is seen
with rocket science, aeronautics, aerodynamics, hydrodynamics and so on.
End








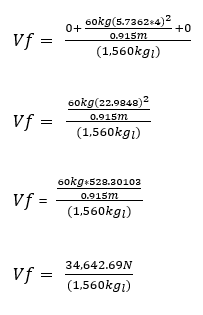








No comments:
Post a Comment